排序算法

冒泡排序

冒泡排序介绍

它是一种较简单的排序算法。它会遍历若干次要排序的数列，每次遍历时，它都会从前往后依次的比较相邻两个数的大小；如果前者比后者大，则交换它们的位置。这样，一次遍历之后，最大的元素就在数列的末尾！ 采用相同的方法再次遍历时，第二大的元素就被排列在最大元素之前。重复此操作，直到整个数列都有序为止！

冒泡排序实现

下面以数列{20,40,30,10,60,50}为例，演示它的冒泡排序过程(如下图)。

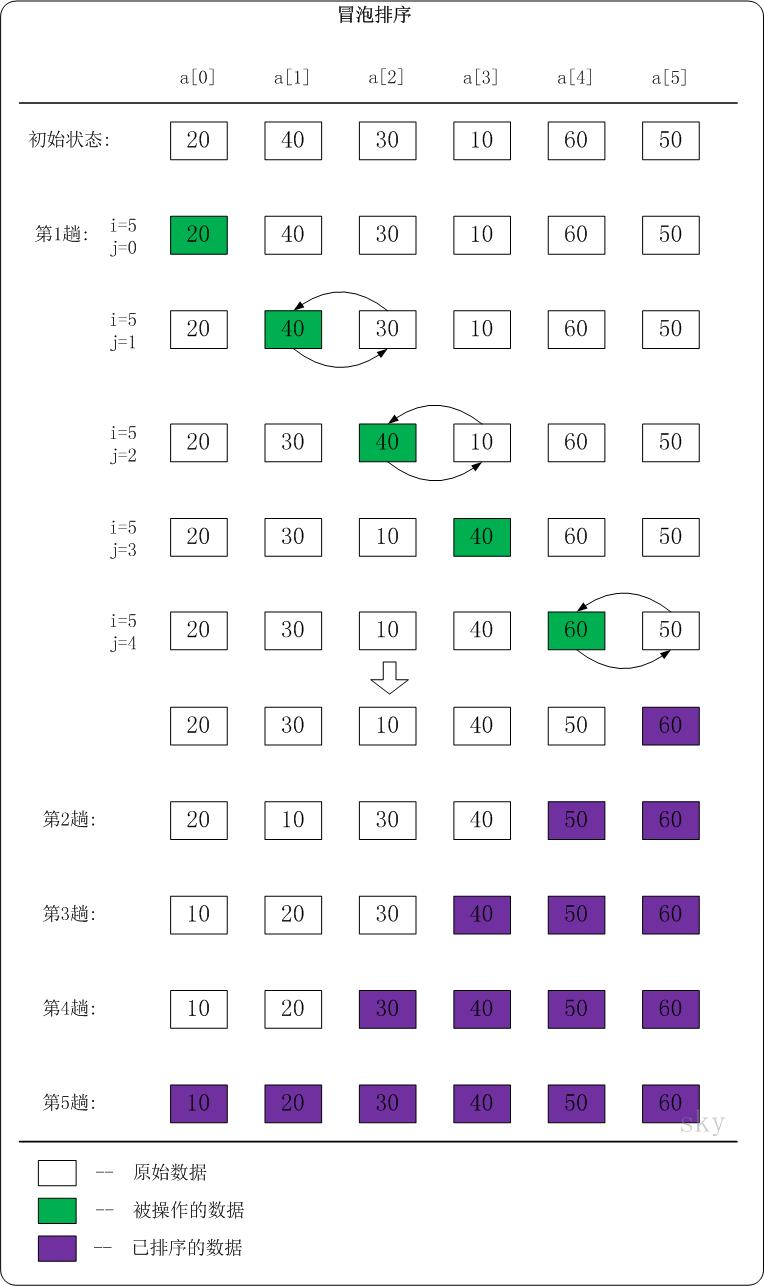
我们先分析第1趟排序

• 当i=5,j=0时，a[0]<a[1]。此时，不做任何处理！
• 当i=5,j=1时，a[1]>a[2]。此时，交换a[1]和a[2]的值；交换之后，a[1]=30，a[2]=40。
• 当i=5,j=2时，a[2]>a[3]。此时，交换a[2]和a[3]的值；交换之后，a[2]=10，a[3]=40。
• 当i=5,j=3时，a[3]<a[4]。此时，不做任何处理！
• 当i=5,j=4时，a[4]>a[5]。此时，交换a[4]和a[5]的值；交换之后，a[4]=50，a[3]=60。

于是，第1趟排序完之后，数列{20,40,30,10,60,50}变成了{20,30,10,40,50,60}。此时，数列末尾的值最大。

根据这种方法:

• 第2趟排序完之后，数列中a[5…6]是有序的。
• 第3趟排序完之后，数列中a[4…6]是有序的。
• 第4趟排序完之后，数列中a[3…6]是有序的。
• 第5趟排序完之后，数列中a[1…6]是有序的。整个数列也就是有序的了。

冒泡排序时间复杂度

冒泡排序的时间复杂度是**O(N^2)**。 假设被排序的数列中有N个数。遍历一趟的时间复杂度是O(N)，需要遍历多少次呢? N-1次！因此，冒泡排序的时间复杂度是O(N^2)。

冒泡排序稳定性

冒泡排序是稳定的算法，它满足稳定算法的定义。

算法稳定性 – 假设在数列中存在a[i]=a[j]，若在排序之前，a[i]在a[j]前面；并且排序之后，a[i]仍然在a[j]前面。则这个排序算法是稳定的！

代码实现

public class BubbleSort {

    /*
     * 冒泡排序
     *
     * 参数说明: 
     *     a -- 待排序的数组
     *     n -- 数组的长度
     */
    public static void bubbleSort1(int[] a, int n) {
        int i,j;

        for (i=n-1; i>0; i--) {
            // 将a[0...i]中最大的数据放在末尾
            for (j=0; j<i; j++) {

                if (a[j] > a[j+1]) {
                    // 交换a[j]和a[j+1]
                    int tmp = a[j];
                    a[j] = a[j+1];
                    a[j+1] = tmp;
                }
            }
        }
    }

    /*
     * 冒泡排序(改进版)
     *
     * 参数说明: 
     *     a -- 待排序的数组
     *     n -- 数组的长度
     */
    public static void bubbleSort2(int[] a, int n) {
        int i,j;
        int flag;                 // 标记

        for (i=n-1; i>0; i--) {

            flag = 0;            // 初始化标记为0
            // 将a[0...i]中最大的数据放在末尾
            for (j=0; j<i; j++) {
                if (a[j] > a[j+1]) {
                    // 交换a[j]和a[j+1]
                    int tmp = a[j];
                    a[j] = a[j+1];
                    a[j+1] = tmp;

                    flag = 1;    // 若发生交换，则设标记为1
                }
            }

            if (flag==0)
                break;            // 若没发生交换，则说明数列已有序。
        }
    }

      /*
     * 冒泡排序
     *
     * 参数说明: 
     *     a -- 待排序的数组
     *     n -- 数组的长度
     */
    public static void bubbleSort3(int[] a, int n){
        int temp;
        for(int i = 0; i < n-1; i++){
            for(int j = 0; j < n-1-i; j++){
                if(a[j] > a[j+1]){
                    temp = a[j];
                    a[j] = a[j+1];
                    a[j+1] = temp;
                }
            }
        }
    }
    
    public static void main(String[] args) {
        int i;
        int[] a = {20,40,30,10,60,50};

        System.out.printf("before sort:");
        for (i=0; i<a.length; i++)
            System.out.printf("%d ", a[i]);
        System.out.printf("\n");

        bubbleSort1(a, a.length);
        //bubbleSort2(a, a.length);

        System.out.printf("after  sort:");
        for (i=0; i<a.length; i++)
            System.out.printf("%d ", a[i]);
        System.out.printf("\n");
    }
}

快速排序

快速排序介绍

它的基本思想是: 选择一个基准数，通过一趟排序将要排序的数据分割成独立的两部分：其中一部分的所有数据都比另外一部分的所有数据都要小。然后，再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

快速排序实现

• 从数列中挑出一个基准值。
• 将所有比基准值小的摆放在基准前面，所有比基准值大的摆在基准的后面(相同的数可以到任一边)；在这个分区退出之后，该基准就处于数列的中间位置。
• 递归地把”基准值前面的子数列”和”基准值后面的子数列”进行排序。

下面以数列a={30,40,60,10,20,50}为例，演示它的快速排序过程(如下图)。

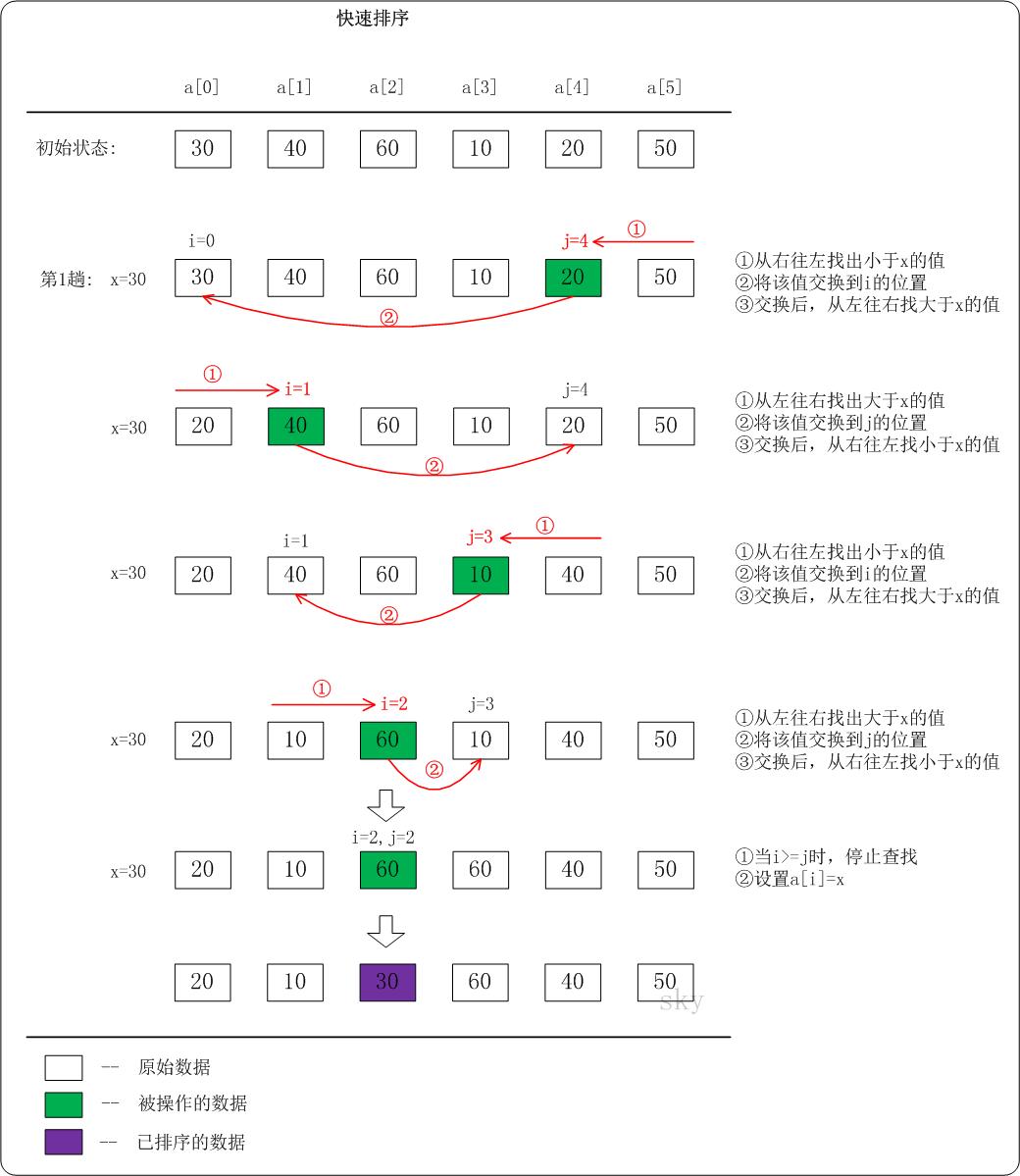
上图只是给出了第1趟快速排序的流程。在第1趟中，设置x=a[i]，即x=30。

• 从”右 –> 左”查找小于x的数: 找到满足条件的数a[j]=20，此时j=4；然后将a[j]赋值a[i]，此时i=0；接着从左往右遍历。
• 从”左 –> 右”查找大于x的数: 找到满足条件的数a[i]=40，此时i=1；然后将a[i]赋值a[j]，此时j=4；接着从右往左遍历。
• 从”右 –> 左”查找小于x的数: 找到满足条件的数a[j]=10，此时j=3；然后将a[j]赋值a[i]，此时i=1；接着从左往右遍历。
• 从”左 –> 右”查找大于x的数: 找到满足条件的数a[i]=60，此时i=2；然后将a[i]赋值a[j]，此时j=3；接着从右往左遍历。
• 从”右 –> 左”查找小于x的数: 没有找到满足条件的数。当i>=j时，停止查找；然后将x赋值给a[i]。此趟遍历结束！

按照同样的方法，对子数列进行递归遍历。最后得到有序数组！

快速排序稳定性

快速排序是不稳定的算法，它不满足稳定算法的定义。

算法稳定性 – 假设在数列中存在a[i]=a[j]，若在排序之前，a[i]在a[j]前面；并且排序之后，a[i]仍然在a[j]前面。则这个排序算法是稳定的！

快速排序时间复杂度

快速排序的时间复杂度在最坏情况下是O(N^2)，平均的时间复杂度是O(N*lgN)。

这句话很好理解: 假设被排序的数列中有N个数。遍历一次的时间复杂度是O(N)，需要遍历多少次呢? 至少lg(N+1)次，最多N次。

• 为什么最少是 lg(N+1) 次? 快速排序是采用的分治法进行遍历的，我们将它看作一棵二叉树，它需要遍历的次数就是二叉树的深度，而根据完全二叉树的定义，它的深度至少是 **lg(N+1)**。因此，快速排序的遍历次数最少是 lg(N+1) 次。
• 为什么最多是N次? 这个应该非常简单，还是将快速排序看作一棵二叉树，它的深度最大是N。因此，快读排序的遍历次数最多是N次。

代码实现

/**
 * 快速排序: Java
 *
 * @author skywang
 * @date 2014/03/11
 */

public class QuickSort {

    /*
     * 快速排序
     *
     * 参数说明: 
     *     a -- 待排序的数组
     *     l -- 数组的左边界(例如，从起始位置开始排序，则l=0)
     *     r -- 数组的右边界(例如，排序截至到数组末尾，则r=a.length-1)
     */
    public static void quickSort(int[] a, int l, int r) {

        if (l < r) {
            int i,j,x;

            i = l;
            j = r;
            x = a[i];
            while (i < j) {
                while(i < j && a[j] > x)
                    j--; // 从右向左找第一个小于x的数
                if(i < j)
                    a[i++] = a[j];
                while(i < j && a[i] < x)
                    i++; // 从左向右找第一个大于x的数
                if(i < j)
                    a[j--] = a[i];
            }
            a[i] = x;
            quickSort(a, l, i-1); /* 递归调用 */
            quickSort(a, i+1, r); /* 递归调用 */
        }
    }

    public static void main(String[] args) {
        int i;
        int a[] = {30,40,60,10,20,50};

        System.out.printf("before sort:");
        for (i=0; i<a.length; i++)
            System.out.printf("%d ", a[i]);
        System.out.printf("\n");

        quickSort(a, 0, a.length-1);

        System.out.printf("after  sort:");
        for (i=0; i<a.length; i++)
            System.out.printf("%d ", a[i]);
        System.out.printf("\n");
    }
}

插入排序

插入排序介绍

直接插入排序(Straight Insertion Sort)的基本思想是: 把 n 个待排序的元素看成为一个有序表和一个无序表。开始时有序表中只包含1个元素，无序表中包含有 n-1 个元素，排序过程中每次从无序表中取出第一个元素，将它插入到有序表中的适当位置，使之成为新的有序表，重复 n-1 次可完成排序过程。

插入排序实现

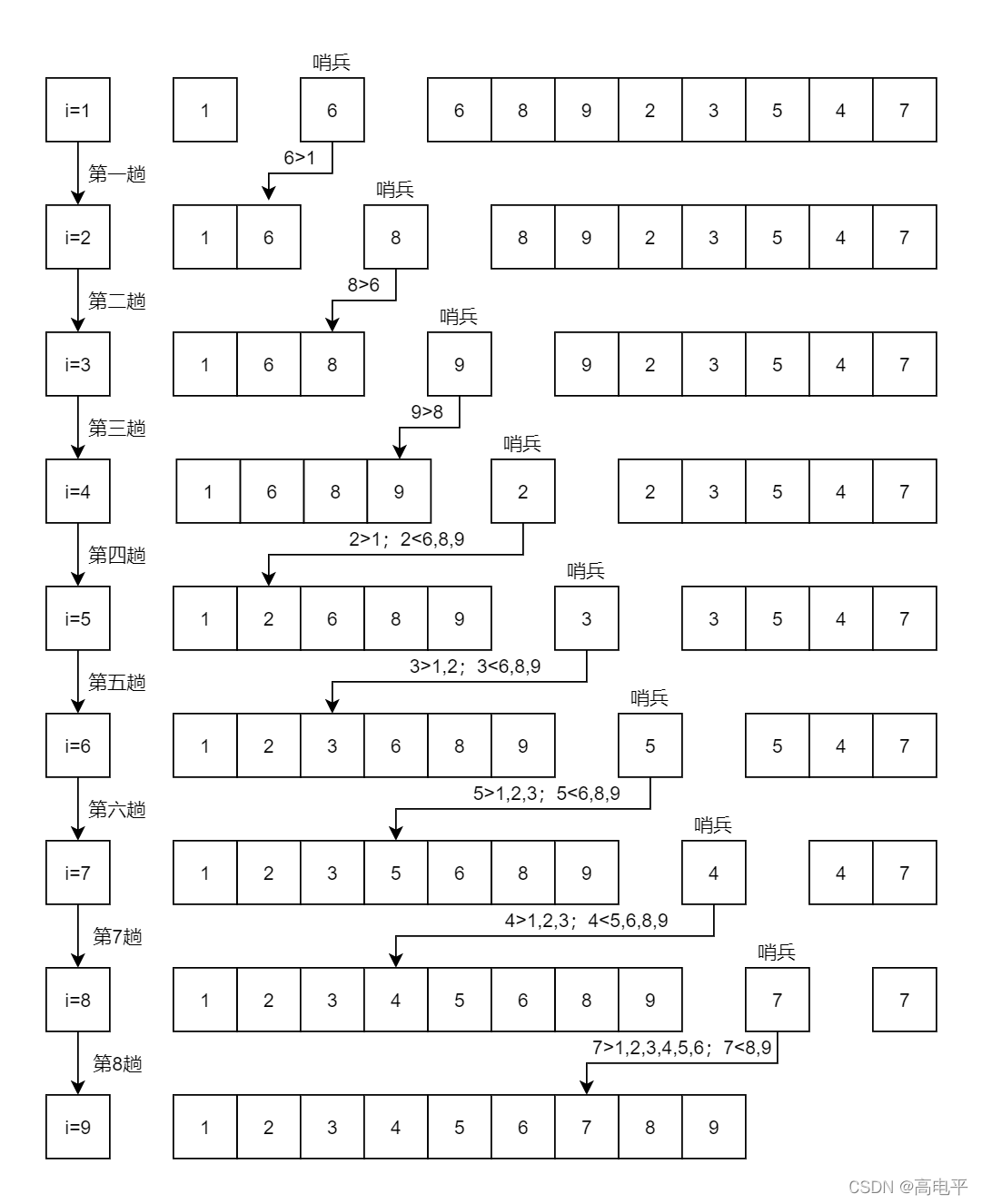
图中将数列分为有序区和无序区。我们需要做的工作只有两个: (1)取出无序区中的第1个数，并找出它在有序区对应的位置。(2)将无序区的数据插入到有序区；若有必要的话，则对有序区中的相关数据进行移位。

插入排序时间复杂度

直接插入排序的时间复杂度是**O(N^2)**。

假设被排序的数列中有N个数。遍历一趟的时间复杂度是O(N)，需要遍历多少次呢? N-1！因此，直接插入排序的时间复杂度是O(N^2)。

插入排序稳定性

直接插入排序是稳定的算法，它满足稳定算法的定义。

算法稳定性 – 假设在数列中存在a[i]=a[j]，若在排序之前，a[i]在a[j]前面；并且排序之后，a[i]仍然在a[j]前面。则这个排序算法是稳定的！

代码实现

/**
 * 直接插入排序: Java
 *
 * @author skywang
 * @date 2014/03/11
 */

public class InsertSort {

    /*
     * 直接插入排序
     *
     * 参数说明: 
     *     a -- 待排序的数组
     *     n -- 数组的长度
     */
    public static void insertSort(int[] a, int n){
        int[] arr = a;
        int len = n;
        for(int i = 1; i < len; i++){ //从第二个元素开始比较
            int temp = arr[i];     //记录当前元素(哨兵)
            for(int j = i - 1; j >= 0; j--){  //从最后一个元素开始比较
                if(arr[j] > temp) {  //如果比当前元素(哨兵)大
                    arr[j + 1] = arr[j]; //从该处往后所有元素向后移动一位
                    arr[j] = temp; //将当前元素(哨兵)插入到arr[j]中
                }
            }
        }
    }
    

    public static void main(String[] args) {
        int i;
        int[] a = {20,40,30,10,60,50};

        System.out.printf("before sort:");
        for (i=0; i<a.length; i++)
            System.out.printf("%d ", a[i]);
        System.out.printf("\n");

        insertSort(a, a.length);

        System.out.printf("after  sort:");
        for (i=0; i<a.length; i++)
            System.out.printf("%d ", a[i]);
        System.out.printf("\n");
    }
}

希尔排序

希尔排序介绍

希尔排序实质上是一种分组插入方法，插入排序经过改进之后的一个更高效的版本。它的基本思想是: 对于 n 个待排序的数列，取一个小于 n 的整数 gap (gap被称为步长)将待排序元素分成若干个组子序列，所有距离为 gap 的倍数的记录放在同一个组中；然后，对各组内的元素进行直接插入排序。 这一趟排序完成之后，每一个组的元素都是有序的。然后减小 gap 的值，并重复执行上述的分组和排序。重复这样的操作，当 gap=1 时，整个数列就是有序的。

希尔排序实现

下面以数列{80,30,60,40,20,10,50,70}为例，演示它的希尔排序过程。

第1趟: (gap=4)

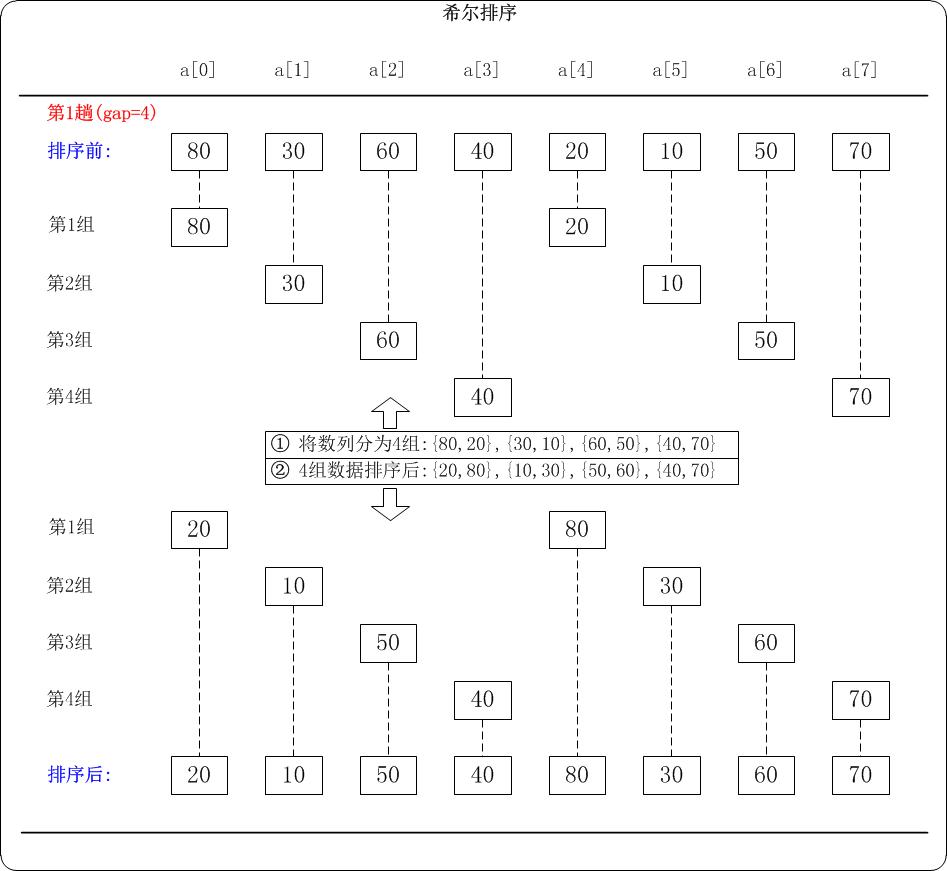
当 gap=4 时,意味着将数列分为4个组: {80,20},{30,10},{60,50},{40,70}。 对应数列: {80,30,60,40,20,10,50,70} 对这4个组分别进行排序，排序结果: {20,80},{10,30},{50,60},{40,70}。 对应数列: {20,10,50,40,80,30,60,70}

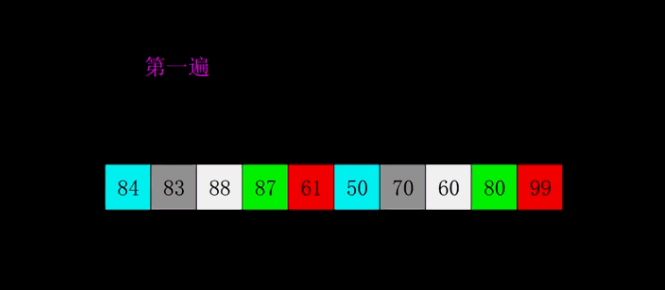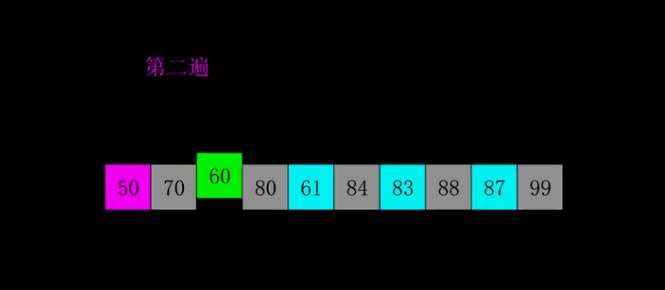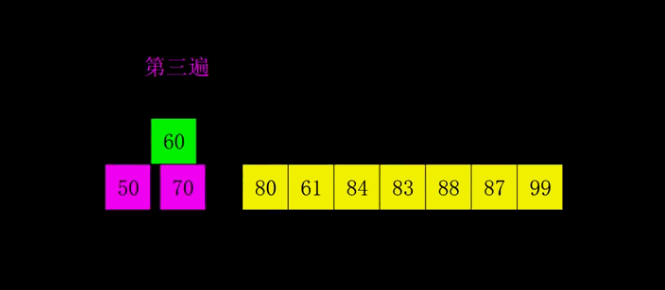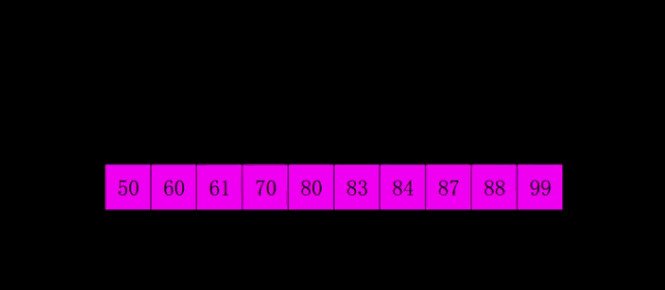
第2趟: (gap=2)

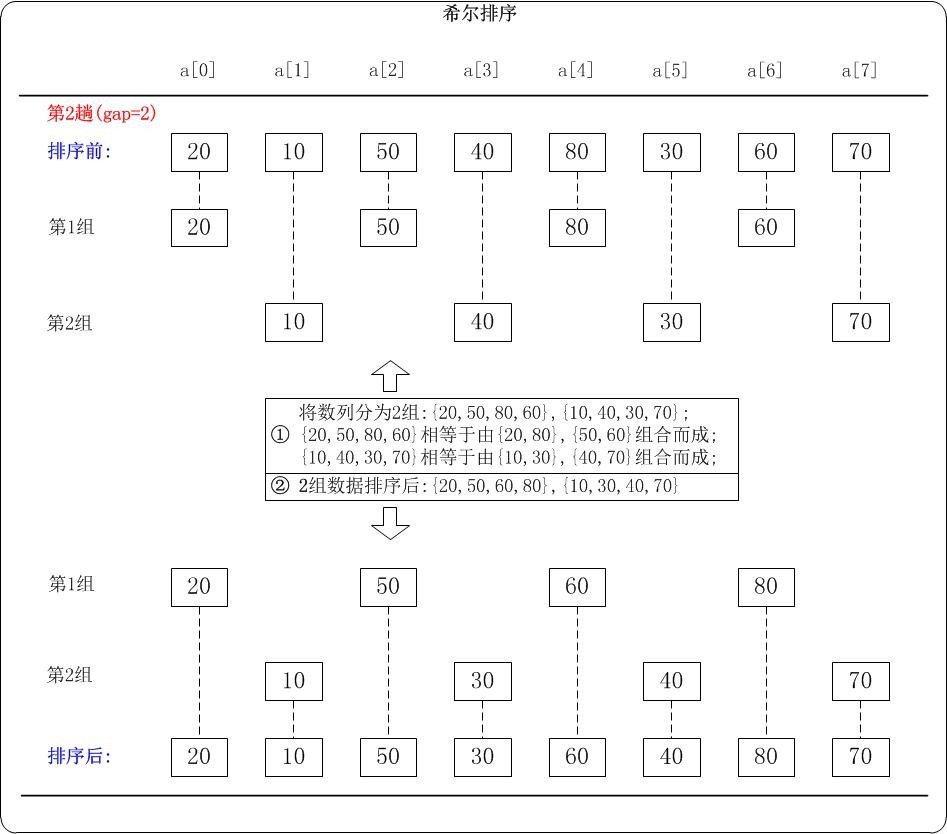
当 gap=2 时,意味着将数列分为2个组: {20,50,80,60}, {10,40,30,70}。 对应数列: {20,10,50,40,80,30,60,70} 注意: {20,50,80,60}实际上有两个有序的数列{20,80}和{50,60}组成。 {10,40,30,70}实际上有两个有序的数列{10,30}和{40,70}组成。 对这2个组分别进行排序，排序结果: {20,50,60,80}, {10,30,40,70}。 对应数列: {20,10,50,30,60,40,80,70}

第3趟: (gap=1)

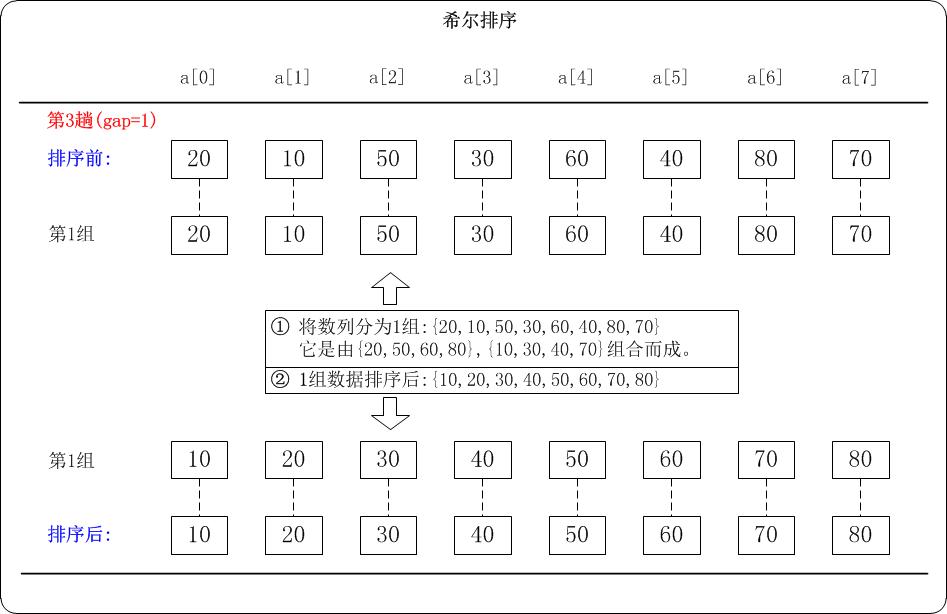
当 gap=1 时,意味着将数列分为1个组: {20,10,50,30,60,40,80,70} 注意: {20,10,50,30,60,40,80,70}实际上有两个有序的数列{20,50,60,80}和{10,30,40,70}组成。 对这1个组分别进行排序，排序结果: {10,20,30,40,50,60,70,80}

希尔排序时间复杂度

希尔排序的时间复杂度与增量(即，步长gap)的选取有关。例如，当增量为1时，希尔排序退化成了直接插入排序，此时的时间复杂度为O(N^2)，而 Hibbard 增量的希尔排序的时间复杂度为O(N3/2)。

希尔排序稳定性

希尔排序是按照不同步长对元素进行插入排序，当刚开始元素很无序的时候，步长最大，所以插入排序的元素个数很少，速度很快；当元素基本有序了，步长很小， 插入排序对于有序的序列效率很高。所以，希尔排序的时间复杂度会比O(n^2)好一些。由于多次插入排序，我们知道一次插入排序是稳定的，不会改变相同元素的相对顺序，但在不同的插入排序过程中，相同的元素可能在各自的插入排序中移动，最后其稳定性就会被打乱，所以shell排序是不稳定的。

算法稳定性 – 假设在数列中存在a[i]=a[j]，若在排序之前，a[i]在a[j]前面；并且排序之后，a[i]仍然在a[j]前面。则这个排序算法是稳定的！

代码实现

public class ShellSort {

    /**
     * 希尔排序
     *
     * 参数说明: 
     *     a -- 待排序的数组
     *     n -- 数组的长度
     */
    public static void shellSort1(int[] a, int n) {

        // gap为步长，每次减为原来的一半。
        for (int gap = n / 2; gap > 0; gap /= 2) {

            // 共 gap个组，对每一组都执行直接插入排序
            for (int i = 0; i < gap; i++) {
                //每个组进行插入排序，用每个组的第二个数进行比较
                for (int j = i + gap; j < n; j += gap) {
                    int temp = a[j];//记录当前元素(哨兵)
                    for(int k = j - gap; k >= 0; k -= gap){  //从最后一个元素开始比较
                        // 如果a[j] < a[j-gap]，则寻找a[j]位置，并将后面数据的位置都后移。
                        if(a[k] > temp) {  //如果比当前元素(哨兵)大
                            a[k + gap] = a[k]; //从该处往后所有元素向后移动一位
                            a[k] = temp; //将当前元素(哨兵)插入到arr[j]中
                        }
                    }
                }
            }
        }
    }

    /**
     * 对希尔排序中的单个组进行排序
     *
     * 参数说明: 
     *     a -- 待排序的数组
     *     n -- 数组总的长度
     *     i -- 组的起始位置
     *     gap -- 组的步长
     *
     *  组是"从i开始，将相隔gap长度的数都取出"所组成的！
     */
    public static void groupSort(int[] a, int n, int i,int gap) {

        for (int j = i + gap; j < n; j += gap) {

            int temp = a[j];//记录当前元素(哨兵)
            for(int k = j - gap; k >= 0; k -= gap){  //从最后一个元素开始比较
                // 如果a[j] < a[j-gap]，则寻找a[j]位置，并将后面数据的位置都后移。
                if(a[k] > temp) {  //如果比当前元素(哨兵)大
                    a[k + gap] = a[k]; //从该处往后所有元素向后移动一位
                    a[k] = temp; //将当前元素(哨兵)插入到arr[j]中
                }
            }
        }
    }

    /**
     * 希尔排序
     *
     * 参数说明: 
     *     a -- 待排序的数组
     *     n -- 数组的长度
     */
    public static void shellSort2(int[] a, int n) {
        // gap为步长，每次减为原来的一半。
        for (int gap = n / 2; gap > 0; gap /= 2) {
            // 共gap个组，对每一组都执行直接插入排序
            for (int i = 0 ;i < gap; i++)
                groupSort(a, n, i, gap);
        }
    }

    public static void main(String[] args) {
        int i;
        int a[] = {80,30,60,40,20,10,50,70};

        System.out.printf("before sort:");
        for (i=0; i< a.length; i++)
            System.out.printf("%d ", a[i]);
        System.out.printf("\n");

        //shellSort1(a, a.length);
        shellSort2(a, a.length);

        System.out.printf("after  sort:");
        for (i=0; i<a.length; i++)
            System.out.printf("%d ", a[i]);
        System.out.printf("\n");
    }
}

选择排序

选择排序介绍

它的基本思想是: 首先在未排序的数列中找到最小(or最大)元素，然后将其存放到数列的起始位置；接着，再从剩余未排序的元素中继续寻找最小(or最大)元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

选择排序实现

1. 将数组的第一个数字设置为标志位最小数并记录最小数下标。
2. 向后遍历，发现更小数后将该数与标志位互换位置并更新最小数与最小数下标。
3. 循环完成排序

下面以数列{1,6,2,3,8,9,5,4,7}为例，演示它的选择排序过程(如下图)。

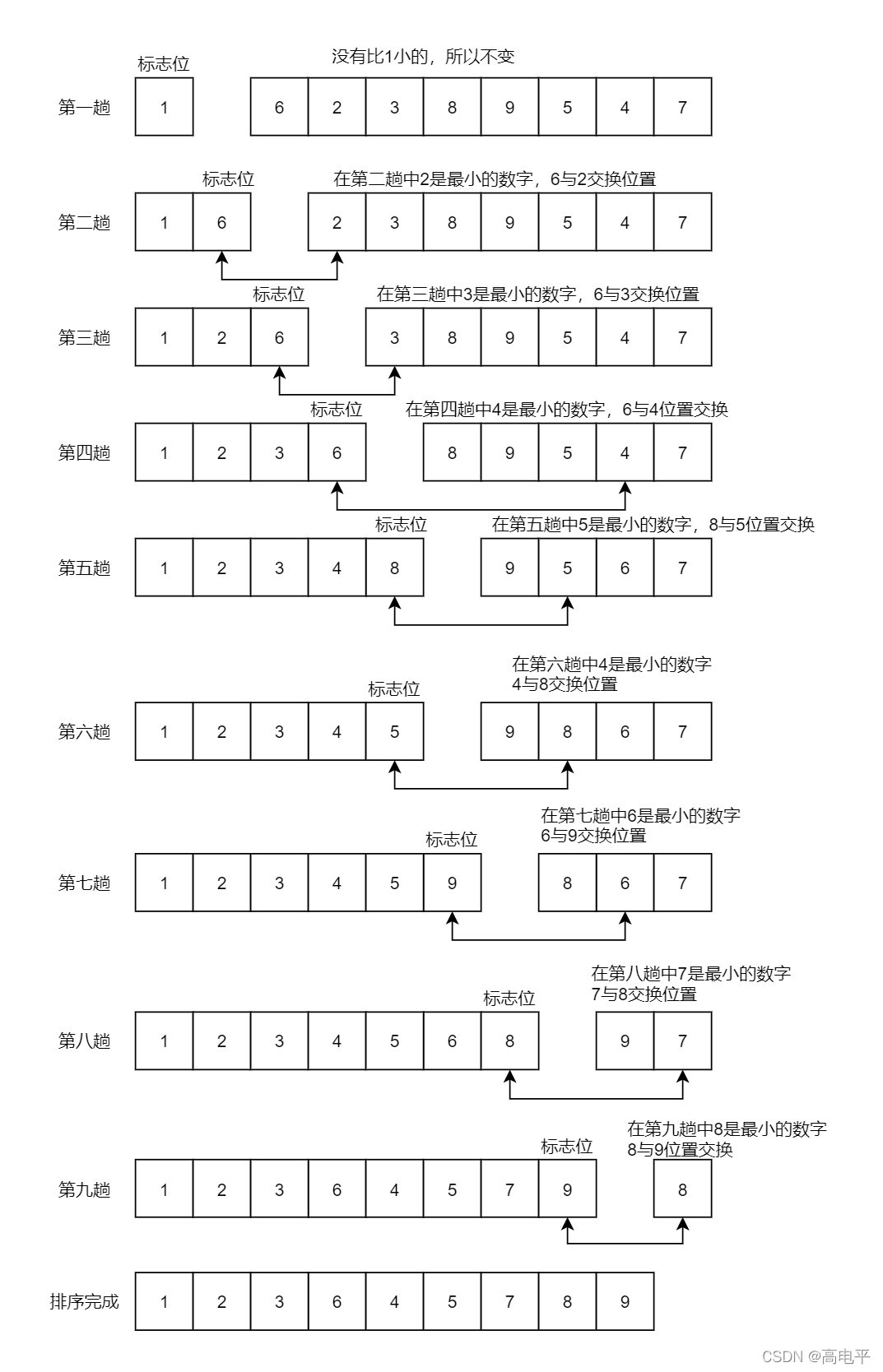
选择排序时间复杂度

选择排序的时间复杂度是O(N^2)。

假设被排序的数列中有N个数。遍历一趟的时间复杂度是O(N)，需要遍历多少次呢? N-1！因此，选择排序的时间复杂度是O(N^2)。

选择排序稳定性

选择排序的稳定性是有一些争议的，不过一般提到排序算法，往往默认是数组实现，所以通常认为选择排序是不稳定的。

• 回顾：什么是排序算法的稳定性？

假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，r[i]=r[j]，且r[i]在r[j]之前，而在排序后的序列中，r[i]仍在r[j]之前，则称这种排序算法是稳定的；否则称为不稳定的。

• 数组实现和链表实现的差异

用数组实现的选择排序是不稳定的，用链表实现的选择排序是稳定的。

不过，一般提到排序算法时，大家往往会默认是数组实现，所以选择排序是不稳定的。

• 此外，排序算法的稳定性也是可以改变的，只是需要额外的时间和空间

有很多办法可以将任意排序算法变成稳定的，但是，往往需要额外的时间或者空间；而我们默认情况谈算法的稳定性是不考虑这种实现的。

代码实现

public class SelectSort {

    public static void main(String[] args) {
        int[] arr = new int[]{1, 6, 8, 9, 2, 3, 5, 4, 7};
        for (int i = 0; i < arr.length - 1; i++) {//每次循环都会找出最小的数
            int minIndex = i;//记录无序数组中最小数的下标
            int minNum = arr[i];//记录无序数组中最小数的值
            for (int j = i + 1; j < arr.length; j++) {//每次循环都会找出最小的数
                if (arr[j] < minNum) {//如果当前数比最小数小，则更新最小数
                    minNum = arr[j];//更新最小数
                    minIndex = j;//更新最小数的下标
                }
            }
            arr[minIndex] = arr[i];//将最小数放到最前面
            arr[i] = minNum;//将标志位放到最小数原来所在的位置
        }

        if(i != minIndex){
            arr[minIndex] = arr[i];//将最小数放到最前面
            arr[i] = minNum;//将标志位放到最小数原来所在的位置
        }
    }
}

堆排序

堆排序介绍

堆分为”最大堆”和”最小堆”。最大堆通常被用来进行”升序”排序，而最小堆通常被用来进行”降序”排序。 鉴于最大堆和最小堆是对称关系，理解其中一种即可。本文将对最大堆实现的升序排序进行详细说明。

最大堆进行升序排序的基本思想:

1. 始化堆: 将数列a[1…n]构造成最大堆，此时，整个序列的最大值就是堆顶的根节点，即a[1]。
2. 交换数据: 将其与末尾元素进行交换，此时末尾就为最大值，即将a[1]和a[n]交换，使a[n]是a[1…n]中的最大值。
3. 然后将a[1…n-1]重新调整为最大堆。 接着，将a[1]和a[n-1]交换，使a[n-1]是a[1…n-1]中的最大值；然后将a[1…n-2]重新调整为最大值。 依次类推，直到整个数列都是有序的。

可以看到在构建大顶堆的过程中，元素的个数逐渐减少，最后就得到一个有序序列了。

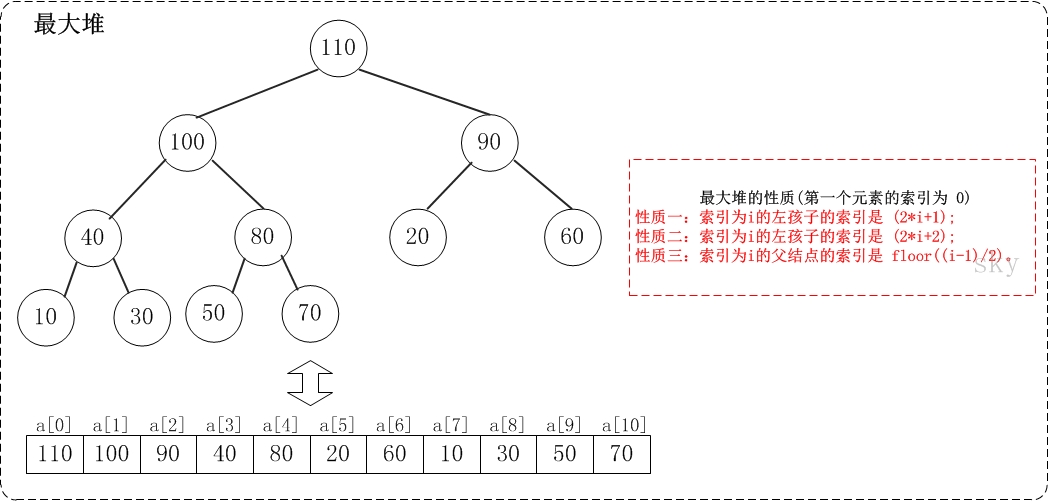
下面，通过图文来解析堆排序的实现过程。注意实现中用到了”数组实现的二叉堆的性质”。 在第一个元素的索引为 0 的情形中:

• 性质一: 索引为 i 的左孩子的索引是 (2*i+1);
• 性质二: 索引为 i 的右孩子的索引是 (2*i+2);
• 性质三: 索引为 i 的父结点的索引是 floor((i-1)/2);

堆排序实现

下面演示heap_sort_asc(a, n)对a={20,30,90,40,70,110,60,10,100,50,80}, n=11进行堆排序过程。下面是数组 a 对应的初始化结构:

初始化堆

在堆排序算法中，首先要将待排序的数组转化成二叉堆。 下面演示将数组 {20,30,90,40,70,110,60,10,100,50,80} 转换为最大堆 {110,100,90,40,80,20,60,10,30,50,70} 的步骤。

1. 从最后一个非叶子结点开始(叶子结点自然不用调整，第一个非叶子结点为 arr.length/2-1=11/2-1=4 ,也就是下面的4结点) , 从右至左,从下至上进行调整。

上面是maxheap_down(a, 4, 9)调整过程。maxheap_down(a, 4, 9)的作用是将a[4…9]进行下调；a[4]的左孩子是a[9]，右孩子是a[10]。调整时，选择左右孩子中较大的一个(即a[10])和a[4]交换。

2. 找到第二个非叶节点 i=3

上面是maxheap_down(a, 3, 9)调整过程。maxheap_down(a, 3, 9)的作用是将a[3…9]进行下调；a[3]的左孩子是a[7]，右孩子是a[8]。调整时，选择左右孩子中较大的一个(即a[8])和a[4]交换。

3. 找到第三个非叶节点 i=2

上面是maxheap_down(a, 2, 9)调整过程。maxheap_down(a, 2, 9)的作用是将a[2…9]进行下调；a[2]的左孩子是a[5]，右孩子是a[6]。调整时，选择左右孩子中较大的一个(即a[5])和a[2]交换。

4. 找到第四个非叶节点 i=1

上面是maxheap_down(a, 1, 9)调整过程。maxheap_down(a, 1, 9)的作用是将a[1…9]进行下调；a[1]的左孩子是a[3]，右孩子是a[4]。调整时，选择左右孩子中较大的一个(即a[3])和a[1]交换。交换之后，a[3]为30，它比它的右孩子a[8]要大，接着，再将它们交换。

5. 找到第五个非叶节点 i=0

上面是maxheap_down(a, 0, 9)调整过程。maxheap_down(a, 0, 9)的作用是将a[0…9]进行下调；a[0]的左孩子是a[1]，右孩子是a[2]。调整时，选择左右孩子中较大的一个(即a[2])和a[0]交换。交换之后，a[2]为20，它比它的左右孩子要大，选择较大的孩子(即左孩子)和a[2]交换。

调整完毕，就得到了最大堆。此时，数组{20,30,90,40,70,110,60,10,100,50,80}也就变成了{110,100,90,40,80,20,60,10,30,50,70}。

交换数据

在将数组转换成最大堆之后，接着要进行交换数据，从而使数组成为一个真正的有序数组。 交换数据部分相对比较简单，下面仅仅给出将最大值放在数组末尾的示意图。

上面是当 n=10 时，交换数据的示意图。 当n=10时，首先交换a[0]和a[10]，使得a[10]是a[0…10]之间的最大值；然后，调整a[0…9]使它称为最大堆。交换之后: a[10]是有序的！ 当n=9时， 首先交换a[0]和a[9]，使得a[9]是a[0…9]之间的最大值；然后，调整a[0…8]使它称为最大堆。交换之后: a[9…10]是有序的！ … 依此类推，直到a[0…10]是有序的。

堆排序时间复杂度

堆排序的时间复杂度是 *O(NlgN)**。

假设被排序的数列中有N个数。遍历一趟的时间复杂度是O(N)，需要遍历多少次呢? 堆排序是采用的二叉堆进行排序的，二叉堆就是一棵二叉树，它需要遍历的次数就是二叉树的深度，而根据完全二叉树的定义，它的深度至少是lg(N+1)。最多是多少呢? 由于二叉堆是完全二叉树，因此，它的深度最多也不会超过lg(2N)。因此，遍历一趟的时间复杂度是O(N)，而遍历次数介于lg(N+1)和lg(2N)之间；因此得出它的时间复杂度是O(N*lgN)。

堆排序稳定性

堆排序是不稳定的算法，它不满足稳定算法的定义。它在交换数据的时候，是比较父结点和子节点之间的数据，所以，即便是存在两个数值相等的兄弟节点，它们的相对顺序在排序也可能发生变化。

算法稳定性 – 假设在数列中存在a[i]=a[j]，若在排序之前，a[i]在a[j]前面；并且排序之后，a[i]仍然在a[j]前面。则这个排序算法是稳定的！

代码实现

public class HeapSort {

    /*
     * (最大)堆的向下调整算法
     *
     * 注: 数组实现的堆中，第N个节点的左孩子的索引值是(2N+1)，右孩子的索引是(2N+2)。
     *     其中，N为数组下标索引值，如数组中第1个数对应的N为0。
     *
     * 参数说明:
     *     a -- 待排序的数组
     *     start -- 被下调节点的起始位置(一般为0，表示从第1个开始)
     *     end   -- 截至范围(一般为数组中最后一个元素的索引)
     */
    public static void maxHeapDown(int[] a, int start, int end) {
        int c = start;            // 当前(current)节点的位置
        int l = 2 * c + 1;        // 左(left)孩子的位置
        int tmp = a[c];            // 当前(current)节点的大小

        for (; l <= end; c = l, l = 2 * l + 1) {
            // "l"是左孩子，"l+1"是右孩子
            if (l < end && a[l] < a[l + 1])
                l++;        // 左右两孩子中选择较大者，即m_heap[l+1]
            if (tmp >= a[l])
                break;        // 调整结束
            else {            // 交换值
                a[c] = a[l];
                a[l] = tmp;
            }
        }
    }

    /*
     * 堆排序(从小到大)
     *
     * 参数说明:
     *     a -- 待排序的数组
     *     n -- 数组的长度
     */
    public static void heapSortAsc(int[] a, int n) {
        int i, tmp;

        // 从(n/2-1) --> 0逐次遍历。遍历之后，得到的数组实际上是一个(最大)二叉堆。
        for (i = n / 2 - 1; i >= 0; i--)
            maxHeapDown(a, i, n - 1);

        // 从最后一个元素开始对序列进行调整，不断的缩小调整的范围直到第一个元素
        for (i = n - 1; i > 0; i--) {
            // 交换a[0]和a[i]。交换后，a[i]是a[0...i]中最大的。
            tmp = a[0];
            a[0] = a[i];
            a[i] = tmp;
            // 调整a[0...i-1]，使得a[0...i-1]仍然是一个最大堆。
            // 即，保证a[i-1]是a[0...i-1]中的最大值。
            maxHeapDown(a, 0, i - 1);
        }
    }

    /*
     * (最小)堆的向下调整算法
     *
     * 注: 数组实现的堆中，第N个节点的左孩子的索引值是(2N+1)，右孩子的索引是(2N+2)。
     *     其中，N为数组下标索引值，如数组中第1个数对应的N为0。
     *
     * 参数说明:
     *     a -- 待排序的数组
     *     start -- 被下调节点的起始位置(一般为0，表示从第1个开始)
     *     end   -- 截至范围(一般为数组中最后一个元素的索引)
     */
    public static void minHeapDown(int[] a, int start, int end) {
        int c = start;            // 当前(current)节点的位置
        int l = 2 * c + 1;        // 左(left)孩子的位置
        int tmp = a[c];            // 当前(current)节点的大小

        for (; l <= end; c = l, l = 2 * l + 1) {
            // "l"是左孩子，"l+1"是右孩子
            if (l < end && a[l] > a[l + 1])
                l++;        // 左右两孩子中选择较小者
            if (tmp <= a[l])
                break;        // 调整结束
            else {            // 交换值
                a[c] = a[l];
                a[l] = tmp;
            }
        }
    }

    /*
     * 堆排序(从大到小)
     *
     * 参数说明:
     *     a -- 待排序的数组
     *     n -- 数组的长度
     */
    public static void heapSortDesc(int[] a, int n) {
        int i, tmp;

        // 从(n/2-1) --> 0逐次遍历每。遍历之后，得到的数组实际上是一个最小堆。
        for (i = n / 2 - 1; i >= 0; i--)
            minHeapDown(a, i, n - 1);

        // 从最后一个元素开始对序列进行调整，不断的缩小调整的范围直到第一个元素
        for (i = n - 1; i > 0; i--) {
            // 交换a[0]和a[i]。交换后，a[i]是a[0...i]中最小的。
            tmp = a[0];
            a[0] = a[i];
            a[i] = tmp;
            // 调整a[0...i-1]，使得a[0...i-1]仍然是一个最小堆。
            // 即，保证a[i-1]是a[0...i-1]中的最小值。
            minHeapDown(a, 0, i - 1);
        }
    }

    public static void main(String[] args) {
        int i;
        int a[] = {20, 30, 90, 40, 70, 110, 60, 10, 100, 50, 80};

        System.out.printf("before sort:");
        for (i = 0; i < a.length; i++)
            System.out.printf("%d ", a[i]);
        System.out.printf("\n");

        heapSortAsc(a, a.length);            // 升序排列
        //heapSortDesc(a, a.length);        // 降序排列

        System.out.printf("after  sort:");
        for (i = 0; i < a.length; i++)
            System.out.printf("%d ", a[i]);
        System.out.printf("\n");
    }
}

归并排序

归并排序介绍

归并排序（Merge sort）是建立在归并操作上的一种有效、稳定的排序算法，该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。根据具体的实现，归并排序包括”从上往下”和”从下往上”2种方式。

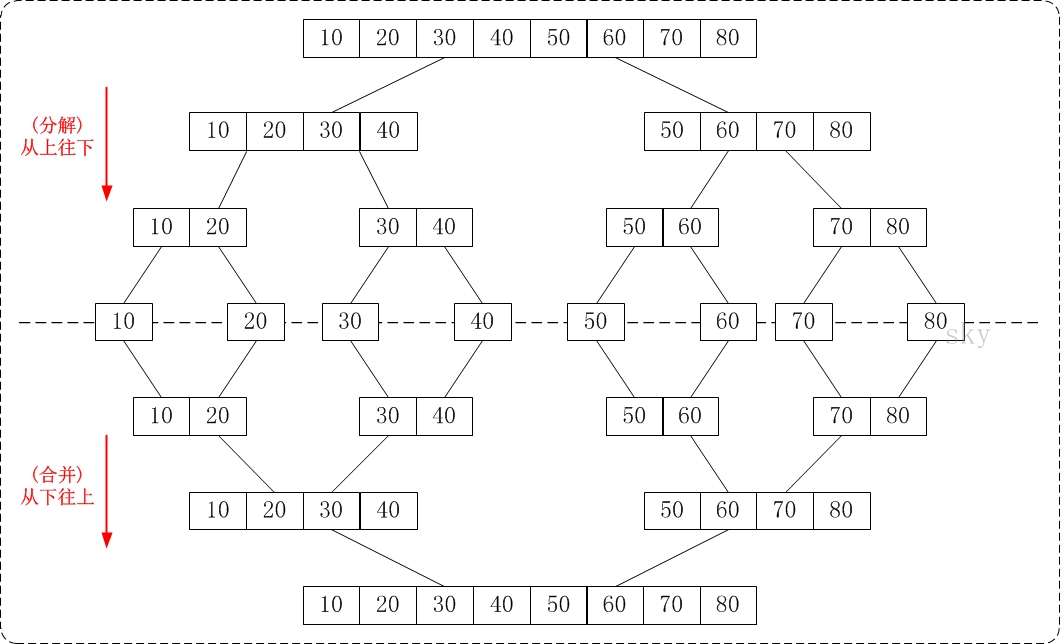
从下往上的归并排序

将待排序的数列分成若干个长度为 1 的子数列，然后将这些数列两两合并；得到若干个长度为 2 的有序数列，再将这些数列两两合并；得到若干个长度为 4 的有序数列，再将它们两两合并；直接合并成一个数列为止。这样就得到了我们想要的排序结果。

从上往下的归并排序

它与”从下往上”在排序上是反方向的。它基本包括3步:

• 分解 – 将当前区间一分为二，即求分裂点 mid = (low + high)/2;
• 求解 – 递归地对两个子区间a[low…mid] 和 a[mid+1…high]进行归并排序。递归的终结条件是子区间长度为1。
• 合并 – 将已排序的两个子区间a[low…mid]和 a[mid+1…high]归并为一个有序的区间a[low…high]。

归并排序实现

从上往下的归并排序

从上往下的归并排序采用了递归的方式实现。它的原理非常简单，如下图:

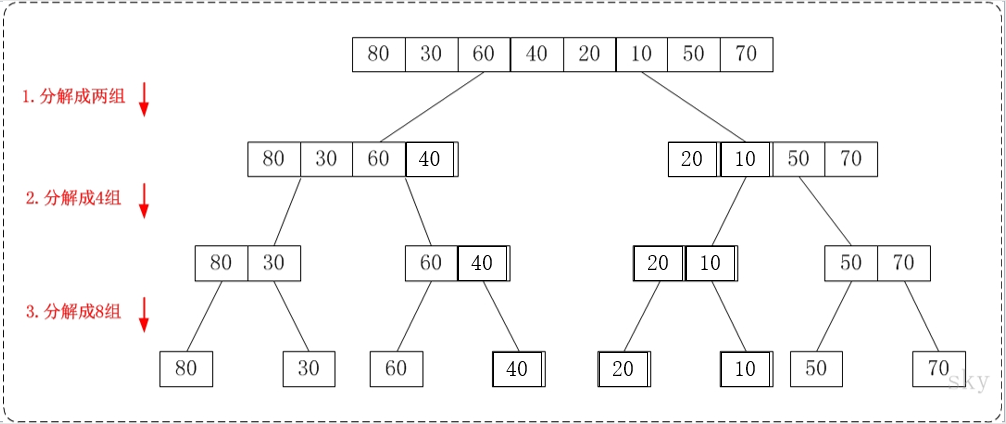
通过”从上往下的归并排序”来对数组{80,30,60,40,20,10,50,70}进行排序时:

• 将数组{80,30,60,40,20,10,50,70}看作由两个有序的子数组{80,30,60,40}和{20,10,50,70}组成。对两个有序子树组进行排序即可。
• 将子数组{80,30,60,40}看作由两个有序的子数组{80,30}和{60,40}组成。将子数组{20,10,50,70}看作由两个有序的子数组{20,10}和{50,70}组成。
• 将子数组{80,30}看作由两个有序的子数组{80}和{30}组成。将子数组{60,40}看作由两个有序的子数组{60}和{40}组成。将子数组{20,10}看作由两个有序的子数组{20}和{10}组成。将子数组{50,70}看作由两个有序的子数组{50}和{70}组成。

从下往上的归并排序

从下往上的归并排序的思想正好与”从下往上的归并排序”相反。如下图:

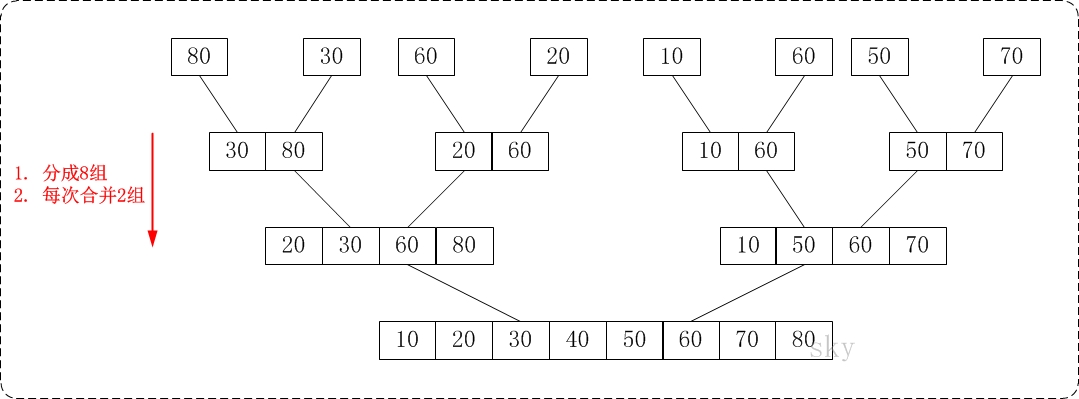
通过”从下往上的归并排序”来对数组{80,30,60,40,20,10,50,70}进行排序时:

• 将数组{80,30,60,40,20,10,50,70}看作由8个有序的子数组{80},{30},{60},{40},{20},{10},{50}和{70}组成。
• 将这8个有序的子数列两两合并。得到4个有序的子树列{30,80},{40,60},{10,20}和{50,70}。
• 将这4个有序的子数列两两合并。得到2个有序的子树列{30,40,60,80}和{10,20,50,70}。
• 将这2个有序的子数列两两合并。得到1个有序的子树列{10,20,30,40,50,60,70,80}。

归并排序时间复杂度

归并排序的时间复杂度是*O(NlgN)**。

假设被排序的数列中有N个数。遍历一趟的时间复杂度是O(N)，需要遍历多少次呢? 归并排序的形式就是一棵二叉树，它需要遍历的次数就是二叉树的深度，而根据完全二叉树的可以得出它的时间复杂度是O(N*lgN)。

归并排序稳定性

归并排序是稳定的算法，它满足稳定算法的定义。

算法稳定性 – 假设在数列中存在a[i]=a[j]，若在排序之前，a[i]在a[j]前面；并且排序之后，a[i]仍然在a[j]前面。则这个排序算法是稳定的！

代码实现

public class MergeSort {

    /*
     * 将一个数组中的两个相邻有序区间合并成一个
     *
     * 参数说明:
     *     a -- 包含两个有序区间的数组
     *     start -- 第1个有序区间的起始地址。
     *     mid   -- 第1个有序区间的结束地址。也是第2个有序区间的起始地址。
     *     end   -- 第2个有序区间的结束地址。
     */
    public static void merge(int[] a, int start, int mid, int end) {
        int[] tmp = new int[end - start + 1];    // tmp是汇总2个有序区的临时区域
        int i = start;            // 第1个有序区的索引
        int j = mid + 1;        // 第2个有序区的索引
        int k = 0;                // 临时区域的索引

        while (i <= mid && j <= end) {
            if (a[i] <= a[j])
                tmp[k++] = a[i++];
            else
                tmp[k++] = a[j++];
        }

        while (i <= mid)
            tmp[k++] = a[i++];

        while (j <= end)
            tmp[k++] = a[j++];

        // 将排序后的元素，全部都整合到数组a中。
        for (i = 0; i < k; i++)
            a[start + i] = tmp[i];

        tmp = null;
    }

    /*
     * 归并排序(从上往下)
     *
     * 参数说明:
     *     a -- 待排序的数组
     *     start -- 数组的起始地址
     *     endi -- 数组的结束地址
     */
    public static void mergeSortUp2Down(int[] a, int start, int end) {
        if (a == null || start >= end)
            return;

        int mid = (end + start) / 2;
        mergeSortUp2Down(a, start, mid); // 递归排序a[start...mid]
        mergeSortUp2Down(a, mid + 1, end); // 递归排序a[mid+1...end]

        // a[start...mid] 和 a[mid...end]是两个有序空间，
        // 将它们排序成一个有序空间a[start...end]
        merge(a, start, mid, end);
    }


    /*
     * 对数组a做若干次合并: 数组a的总长度为len，将它分为若干个长度为gap的子数组；
     *             将"每2个相邻的子数组" 进行合并排序。
     *
     * 参数说明:
     *     a -- 待排序的数组
     *     len -- 数组的长度
     *     gap -- 子数组的长度
     */
    public static void mergeGroups(int[] a, int len, int gap) {
        int i;
        int twolen = 2 * gap;    // 两个相邻的子数组的长度

        // 将"每2个相邻的子数组" 进行合并排序。
        for (i = 0; i + 2 * gap - 1 < len; i += (2 * gap))
            merge(a, i, i + gap - 1, i + 2 * gap - 1);

        // 若 i+gap-1 < len-1，则剩余一个子数组没有配对。
        // 将该子数组合并到已排序的数组中。
        if (i + gap - 1 < len - 1)
            merge(a, i, i + gap - 1, len - 1);
    }

    /*
     * 归并排序(从下往上)
     *
     * 参数说明:
     *     a -- 待排序的数组
     */
    public static void mergeSortDown2Up(int[] a) {
        if (a == null)
            return;

        for (int n = 1; n < a.length; n *= 2)
            mergeGroups(a, a.length, n);
    }

    public static void main(String[] args) {
        int i;
        int a[] = {80, 30, 60, 40, 20, 10, 50, 70};

        System.out.printf("before sort:");
        for (i = 0; i < a.length; i++)
            System.out.printf("%d ", a[i]);
        System.out.printf("\n");

        mergeSortUp2Down(a, 0, a.length-1);        // 归并排序(从上往下)
        //mergeSortDown2Up(a);                    // 归并排序(从下往上)

        System.out.printf("after  sort:");
        for (i = 0; i < a.length; i++)
            System.out.printf("%d ", a[i]);
        System.out.printf("\n");
    }
}

桶排序

桶排序介绍

假设待排序的数组 a 中共有 N 个整数，并且已知数组 a 中数据的范围[0, MAX)。在桶排序时，创建容量为MAX的桶数组 r，并将桶数组元素都初始化为0；将容量为 MAX 的桶数组中的每一个单元都看作一个”桶”。

在排序时，逐个遍历数组a，将数组 a 的值，作为”桶数组r”的下标。当 a 中数据被读取时，就将桶的值加1。例如，读取到数组a[3]=5，则将r[5]的值+1。

桶排序实现

假设a={8,2,3,4,3,6,6,3,9}, max=10。此时，将数组a的所有数据都放到需要为0-9的桶中。如下图:

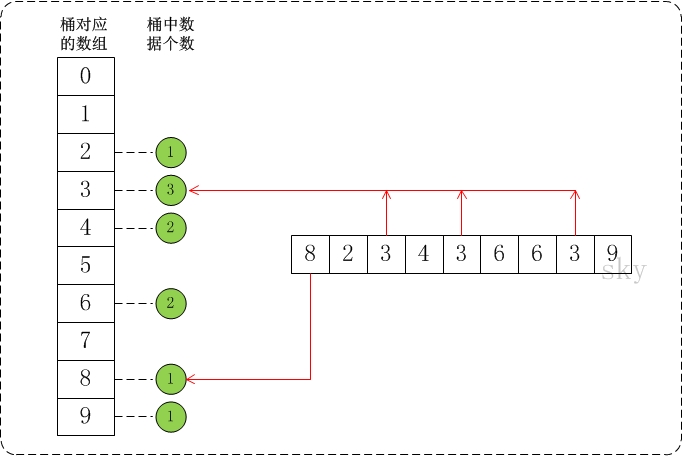
在将数据放到桶中之后，再通过一定的算法，将桶中的数据提出来并转换成有序数组。就得到我们想要的结果了。

桶排序复杂度

• 平均时间复杂度: O(n + k)，n为待排元素数，k为桶数。
• 最佳时间复杂度: O(n + k)
• 最差时间复杂度: O(n ^ 2)
• 空间复杂度: O(n * k)

桶排序最好情况下使用线性时间O(n)，桶排序的时间复杂度，取决与对各个桶之间数据进行排序的时间复杂度，因为其它部分的时间复杂度都为O(n)。很显然，桶划分的越小，各个桶之间的数据越少，排序所用的时间也会越少。但相应的空间消耗就会增大。

桶排序稳定性

稳定性: 稳定

代码实现

public class BucketSort {

    /*
     * 桶排序
     *
     * 参数说明:
     *     a -- 待排序数组
     *     max -- 数组a中最大值的范围
     */
    public static void bucketSort(int[] a, int max) {
        int[] buckets;

        if (a == null || max < 1)
            return;

        // 创建一个容量为max的数组buckets，并且将buckets中的所有数据都初始化为0。
        buckets = new int[max];

        // 1. 计数
        for (int i = 0; i < a.length; i++)
            buckets[a[i]]++;

        // 2. 排序
        for (int i = 0, j = 0; i < max; i++) {
            while ((buckets[i]--) > 0) {
                a[j++] = i;
            }

            buckets = null;
        }
    }

    public static void main(String[] args) {
        int i;
        int a[] = {8, 2, 3, 4, 3, 6, 6, 3, 9};

        System.out.printf("before sort:");
        for (i = 0; i < a.length; i++)
            System.out.printf("%d ", a[i]);
        System.out.printf("\n");

        bucketSort(a, 10); // 桶排序

        System.out.printf("after  sort:");
        for (i = 0; i < a.length; i++)
            System.out.printf("%d ", a[i]);
        System.out.printf("\n");
    }
}

基数排序

基数排序介绍

基数排序是桶排序的扩展，它的基本思想是: 将整数按位数切割成不同的数字，然后按每个位数分别比较。 具体做法是: 将所有待比较数值统一为同样的数位长度，数位较短的数前面补零。然后，从最低位开始，依次进行一次排序。这样从最低位排序一直到最高位排序完成以后, 数列就变成一个有序序列。

基数排序实现

通过基数排序对数组{389, 12, 3, 36, 66, 89, 13, 30}

1. 准备足够的存储空间，bucket存放数字，elementCount计数。

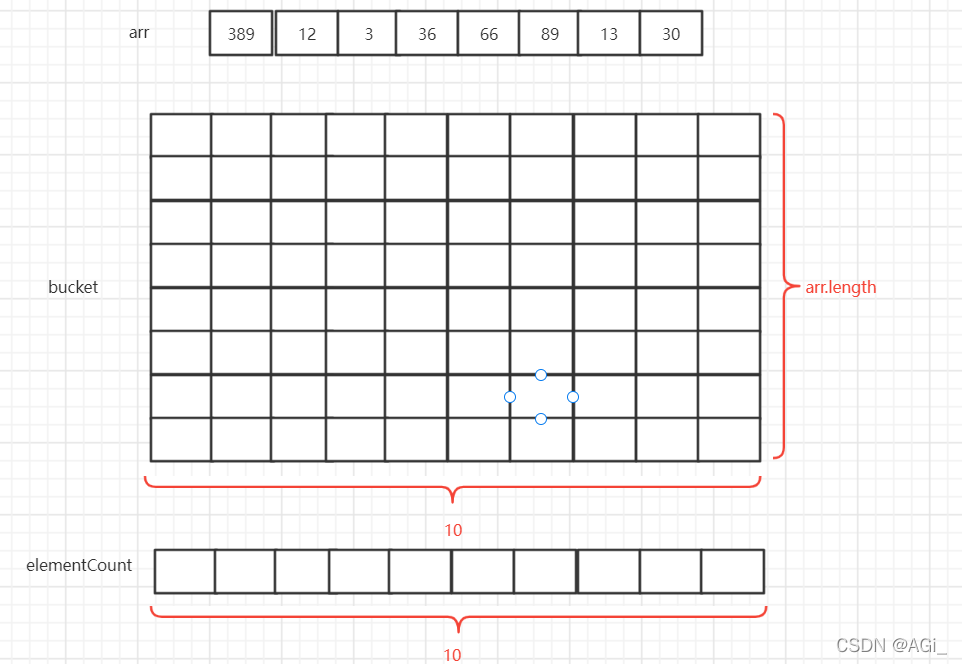
2. 第一次循环，把每个数先除1，再除10求余数，余数是几就把该数据放到下标是几的数组里面，对应的elementCount加一。

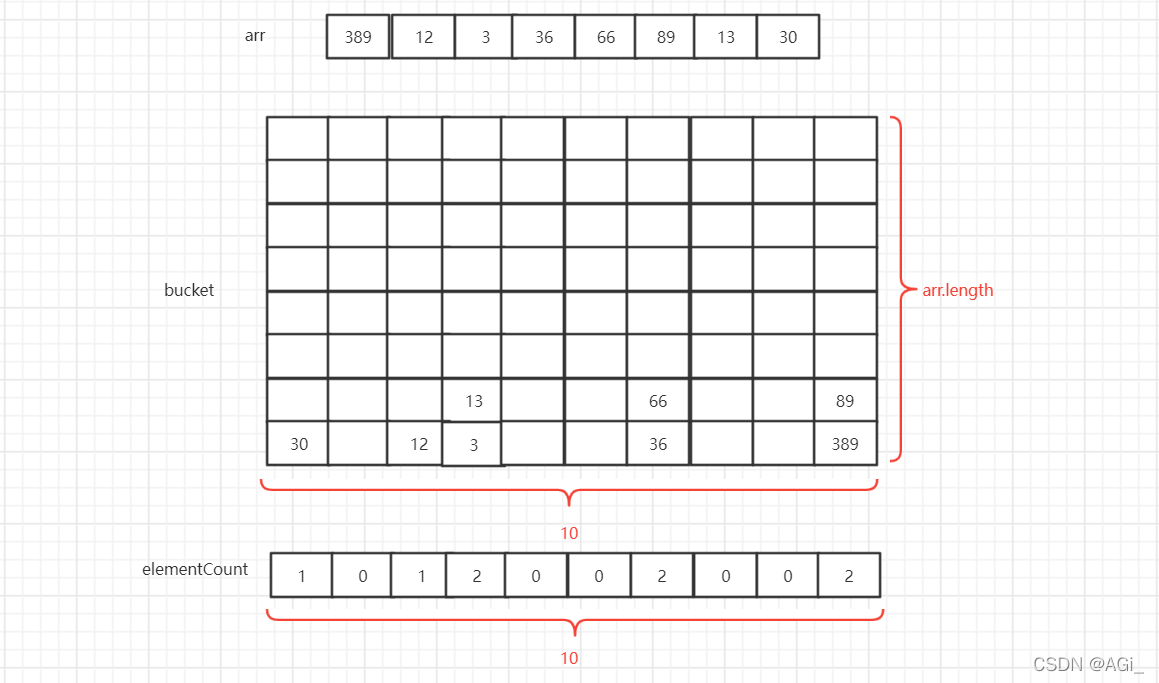
3. 依次把数据从bucket里面拿出来，然后依次填回arr数组里面里面。elementCount置零。

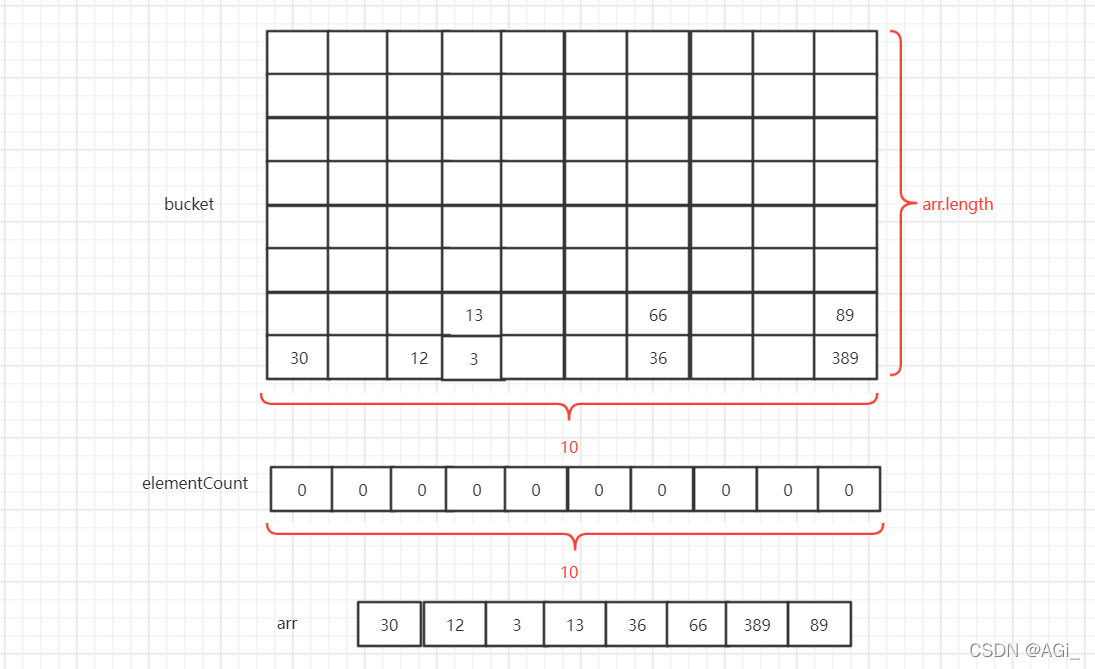
arr数组是按个位数有序的。

4. 第二次循环，把每个数先除10，再除10求余数，余数是几就把该数据放到下标是几的数组里面，对应的elementCount加一。

基数排序复杂度

O(d(r+n))，r 代表关键字的基数，d 代表长度，n 代表关键字的个数

基数排序稳定性

稳定

代码实现

• 确定最大数的位数

int max=arr[0];
for(int i=0;i<arr.length;i++) {
	if(arr[i]>max) {
		max=arr[i];
	}
}
int maxLength=(max+"").length();

public class RadixSort {
    //基数排序
    public static void main(String[] args) {
        // TODO Auto-generated method stub
        int[] arr = {4, 3, 7, 4, 9, 2, 10};
        System.out.println(Arrays.toString(arr));
        sort(arr);
        System.out.println(Arrays.toString(arr));
    }

    public static void sort(int[] arr) {
        int max = arr[0]; //假设第一个数就是最大数
        for (int i = 0; i < arr.length; i++) {
            if (arr[i] > max) {
                max = arr[i];
            }
        }
        //获取最大值的位数
        int maxLength = (max + "").length();
        //申请所需要的内存空间
        //第一轮（针对每个元素的个位进行排序处理）
        //定义一个二维数组，表示10个桶，每个桶就是一维数组
        //说明：
        //1.二维数组包含10个一维数组
        //2.为了防止在放入数的时候，数据溢出，则每个一个数组（桶），大小定为arr.length
        int[][] bucket = new int[10][arr.length];
        //了记录每个桶中，实际存放了多少个数据，我们定义了一个一维数组来记录各个桶中的个数
        int[] elementCount = new int[10];

        int n = 1;
        for (int h = 0; h < maxLength; h++) {
            //基数排序的核心是下面两个for循环
            for (int i = 0; i < arr.length; i++) {
                //取出每个元素的对应位的值进行排序处理，第一次是个位，第二次是十位。。。
                int element = arr[i] / n % 10;
                //放入到对应的桶中
                bucket[element][elementCount[element]] = arr[i];
                elementCount[element]++;
            }

            //按照这个桶的顺序（一维数组的下标依次取出数据，放入原来数组）
            int index = 0;
            //遍历每一桶，并将桶中的数据，放入到原数组
            for (int k = 0; k < elementCount.length; k++) {
                //如果桶中，有数据，我们才能放入到原数组
                if (elementCount[k] != 0) {
                    //循环该桶即第k个桶，（即第k个一维数组），放入
                    for (int i = 0; i < elementCount[k]; i++) {
                        //取出元素放入arr
                        arr[index] = bucket[k][i];
                        index++;
                    }
                }
                //第i+1轮处理后，需要将每个elementCount[k]=0!!!
                elementCount[k] = 0;
            }
            n = n * 10;
        }

    }
}